ミニクイズのこたえ

問題

背景のタイルには、グレーに塗られた３つ組のタイルがたくさんあります。決まったルールで塗られていますが、１か所だけ間違って塗られているところがあります。それはどこでしょう？

答

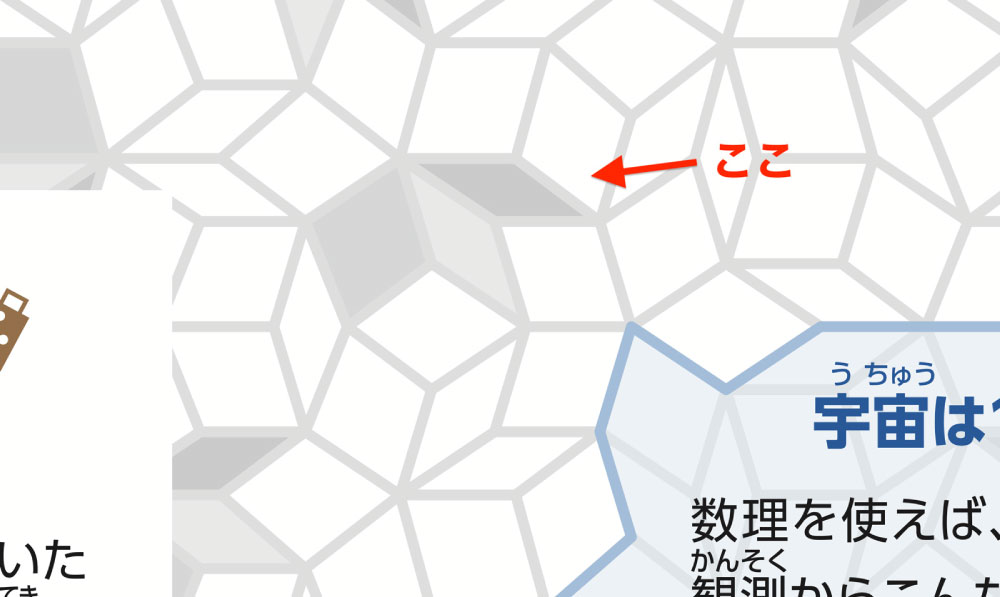
「宇宙は138億歳」の左上。ここです。

解説

問題にもある通り、この３つ組はある決まったルールで塗られているので、まずそのルールを見つけることが、答を探すための糸口になります。

３つ組のタイルを見ると、どれも同じ形をしています。細い・細い・太い、という３枚のタイルの並びですが、３枚が集まった頂点に注目してください。この頂点には、７枚のタイルが集まっていて、先程の３枚から時計回りに見ると、細・細・太・太・細・細・太、となっています。（図では分かりやすいように色を変えました）

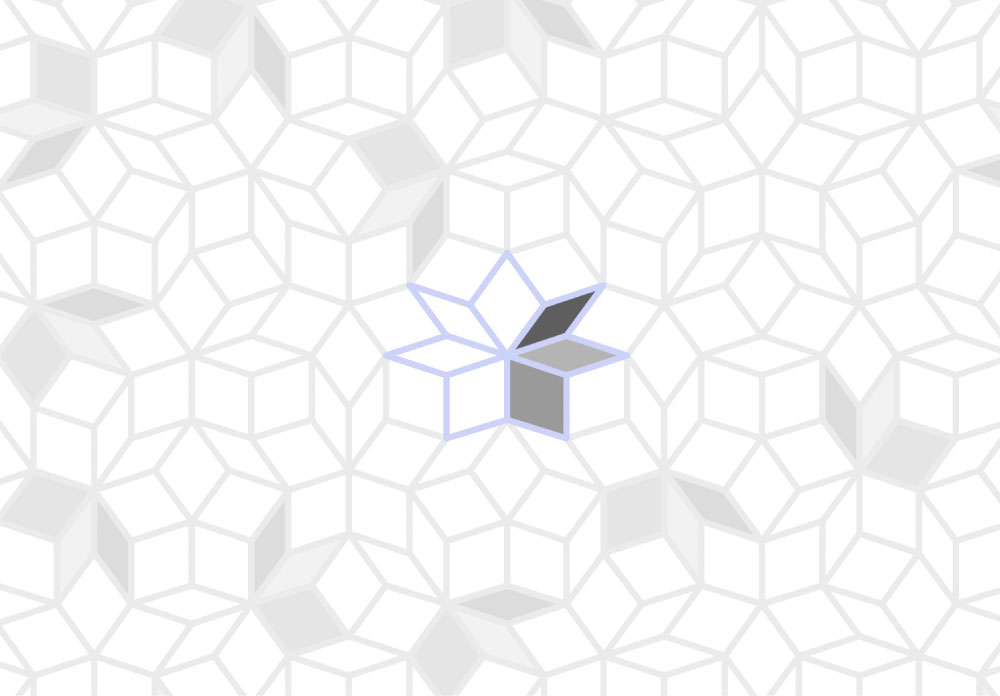
背景のタイル模様の頂点には、集まるタイルの数が３枚から７枚まで、いろいろありますが、７枚集まる頂点は、タイルが必ずこの並びになっています。３つ組は、その最初の「細・細・太」だけに色を付けたものだったのです。

あらためて、正解に上げた「宇宙は138億歳」の左上にある三つ組を見てください。３つ組の形は同じですが、頂点に注目すると、タイルが６枚しか集まっていません。したがって、これが塗り間違えたタイルだ、ということが分かります。

ペンローズ・タイルについて

背景に使われているタイル模様は、ペンローズ・タイルという２種類のひし形を、すき間なくならべてできた模様になっています。このタイルの辺には区別があり、図のように辺の色と向きをそろえて並べると、どれだけ広くならべても同じパターンの繰り返しが絶対に起こらない、というおもしろい性質があります。

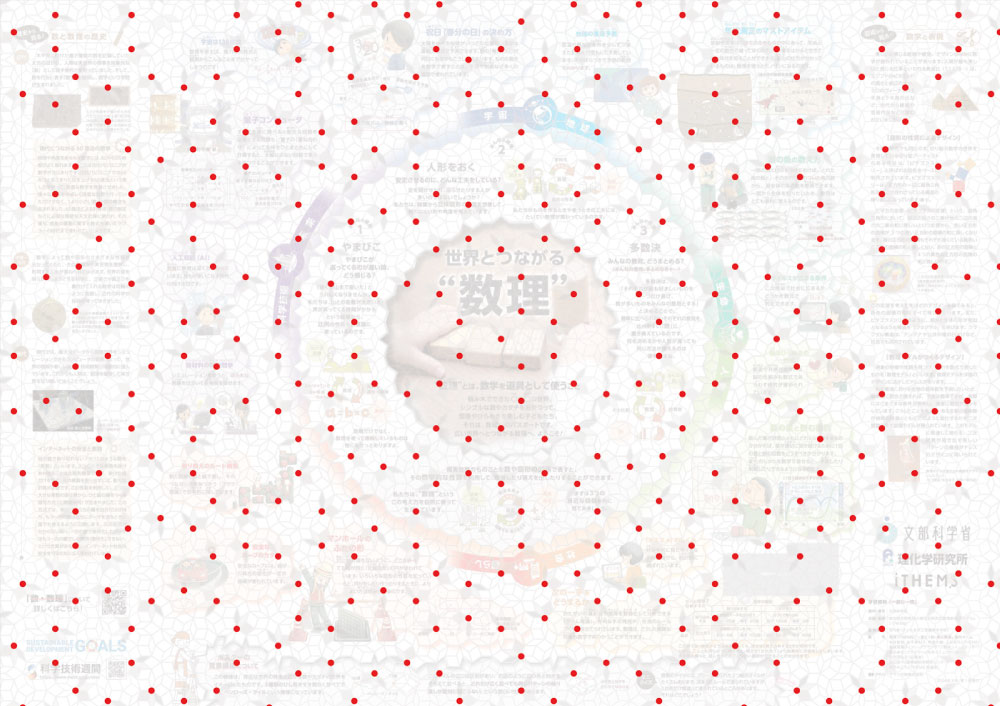
以下の図は、ポスターの３つ組が集まった頂点に赤い印を付けたものです。ぱっと目にはわかりにくいですが、縦方向にも横方向にも、繰り返しにはなっていません。それでも、何となく、何かの規則性があるようにも見えるのが不思議ですね。